7  Probability, statistics, and simulations

7.1 What is probability?

  • Informally, a probability is a number that describes how likely an event is.
    • It is, by definition, between 0 and 1.
    • What is the probability that a fair coin flip will result in heads?
  • We can also think of a probability as an outcome’s relative frequency after repeating an “experiment” many times.1
    • In this setting, an experiment is “an action or a set of actions that produce stochastic [random] events of interest” (Imai and Williams 2022, p. 281). Not to confuse with scientific experiments!
    • If we were to flip a million fair coins, what will be the proportion of heads?
  • A probability space \((\Omega, S, P)\) is a formal way to talk about a random process:
    • The sample space (\(\Omega\)) is the set of all possible outcomes.
    • The event space (\(S\)) is a collection of events (an event is a subset of \(\Omega\)).
    • The probability measure (\(P\)) is a function that assigns a probability in \(\mathbb{R}\) to every event in \(S\). So \(P: S \rightarrow \mathbb{R}\).
  • We can formalize our intuitions with the probability axioms (sometimes called Kolmogorov’s axioms):
    • \(P(A) \ge 0, \; \forall A \in S\).
      • Probabilities must be non-negative.
    • \(P(\Omega) = 1\).
      • Something has to happen!
      • Probabilities sum/integrate to 1.
    • \(P(A \cup B) = P(A) + P(B), \; \forall A, B \in S, \; A\cup B = \emptyset\).
      • The probability of disjoint (mutually exclusive) events is equal to the sum of their individual probabilities.

7.1.1 Definitions and properties of probability

  • Joint probability: \(P(A \cap B)\). The probability that the two events will occur in one realization of the experiment.

  • Law of total probability: \(P(A) = P(A \cap B) + P(A \cap B^C)\).

  • Addition rule: \(P(A \cup B) = P(A) + P(B) - P (A \cap B)\).

  • Conditional probability: \(\displaystyle P(A|B)=\frac{P(A \cap B)}{P(B)}\)

  • Bayes theorem: \(\displaystyle P(A|B) = \frac{P(A) \cdot P(B|A)}{P(B)}\)

7.1.2 Random variables and probability distributions

  • A random variable is a function (\(X: \Omega \to \mathbb{R}\)) of the outcome of a random generative process. Informally, it is a “placeholder” for whatever will be the output of a process we’re studying.

  • A probability distribution describes the probabilities associated with the values of a random variable.

  • Random variables (and probability distributions) can be discrete or continuous.

7.1.2.1 Discrete random variables and probability distributions

  • A sample space in which there are a (finite or infinite) countable number of outcomes

  • Each realization of random process has a discrete probability of occurring.

    • \(f(X=x_i)=P(X=x_i)\) is the probability the variable takes the value \(x_i\).
An example

  • What’s the probability that we’ll roll a 3 on one die roll: \[Pr(y=3) = \dfrac{1}{6}\]

  • If one roll of the die is an “experiment,” we can think of a 3 as a “success.”

  • \(Y \sim Bernoulli \left(\frac{1}{6} \right)\)

  • Fair coins are \(\sim Bernoulli(.5)\), for example.

  • More generally, \(Bernoulli(\pi )\). We’ll talk about other probability distributions soon.

    • \(\pi\) represents the probability of success.

Let’s do another example on the board, using the sum of two fair dice.

7.1.2.2 Continuous random variables and probability distributions

  • What happens when our outcome is continuous?
  • There are an infinite number of outcomes. This makes the denominator of our fraction difficult to work with.
  • The probability of the whole space must equal 1.
  • The domain may not span -\(\infty\) to \(\infty\).
    • Even space between 0 and 1 is infinite!
  • Two common examples are the uniform and normal probability distributions, which we will discuss below.

7.1.3 Functions describing probability distributions

7.1.3.1 Probability Mass Function (PMF)

Probability of each occurrence encoded in probability mass function (PMF)

  • \(0 \leq f(x_i) \leq 1\)
    • Probability of any value occurring must be between 0 and 1.
  • \(\displaystyle\sum_{x}f(x_i) = 1\)
    • Probabilities of all values must sum to 1.

7.1.3.2 Probability Density Function (PDF)

  • Similar to PMF from before, but for continuous variables.
  • Using integration, it gives the probability a value falls within a particular interval
    • \(P[a\le X\le b] = \displaystyle\int_a^b f(x) \, dx\)
    • Total area under the curve is 1.
    • \(P(a < X < b)\) is the area under the curve between \(a\) and \(b\) (where \(b > a\)).

7.1.3.3 Cumulative Density Function (CDF)

Discrete
  • Cumulatve density function is probability X will take a value of x or lower.
  • PDF is written \(f(x)\), and CDF is written \(F'(x)\). \[F_X(x) = Pr(X\leq x)\]
  • For discrete CDFs, that means summing up over all values.
  • What is the probability of rolling a 6 or lower with two dice? \(F(6)=?\)
Continuous
  • We can’t sum probabilities for continuous distributions (remember the 0 problem).
  • Solution: integration \[F_Y(y) = \int_{-\infty}^{y} f(y) dy\]
  • Examples of uniform distribution.

7.1.4 Common types of probability distributions

There are many useful probability distributions. In this section we will cover three of the most common ones: the binomial, uniform, and normal distributions.

7.1.4.1 Binomial distribution

A Binomial distribution is defined as follow: \(X \sim Binomial(n, p)\)

PMF:

\[ {n \choose k} p^k(1-p)^{n-k} \] , where \(n\) is the number of trials, \(p\) is the probability of success, and \(k\) is the number of successes.

Remember that:

\[ {n \choose k} = \frac{n!}{k!(n-k)!} \]

For example, let’s say that voters choose some candidate with probability 0.02. What is the probability of seeing exactly 0 voters of the candidate in a sample of 100 people?

We can compute the PMF of a binomial distribution using R’s dbinom() function.

dbinom(x = 0, size = 100, prob = 0.02)
[1] 0.1326196
dbinom(x = 1, size = 100, prob = 0.02)
[1] 0.2706522

Similarly, we can compute the CDF using R’s pbinom() function:

pbinom(q = 0, size = 100, prob = 0.02)
[1] 0.1326196
pbinom(q = 100, size = 100, prob = 0.02)
[1] 1
pbinom(q = 1, size = 100, prob = 0.02)
[1] 0.4032717
Exercise

Compute the probability of seeing between 1 and 10 voters of the candidate in a sample of 100 people.

7.1.4.2 Uniform distribution

A uniform distribution has two parameters: a minimum and a maximum. So \(X \sim U(a, b)\).

  • PDF:

\[ \displaystyle{ \begin{cases} \frac{1}{b-a} & \text{, }{x \in [a, b]}\\ 0 & \text{, otherwise} \end{cases} } \]

  • CDF:

\[ \displaystyle{ \begin{cases} 0 & \text{, }{x < a}\\ \frac{x-a}{b-a} & \text{, }{x \in [a, b]}\\ 1 & \text{, }{x>b} \end{cases} } \]

In R, dunif() gives the PDF of a uniform distribution. By default, it is \(X \sim U(0, 1)\).

library(tidyverse)
ggplot() +
  stat_function(fun = dunif, xlim = c(-4, 4))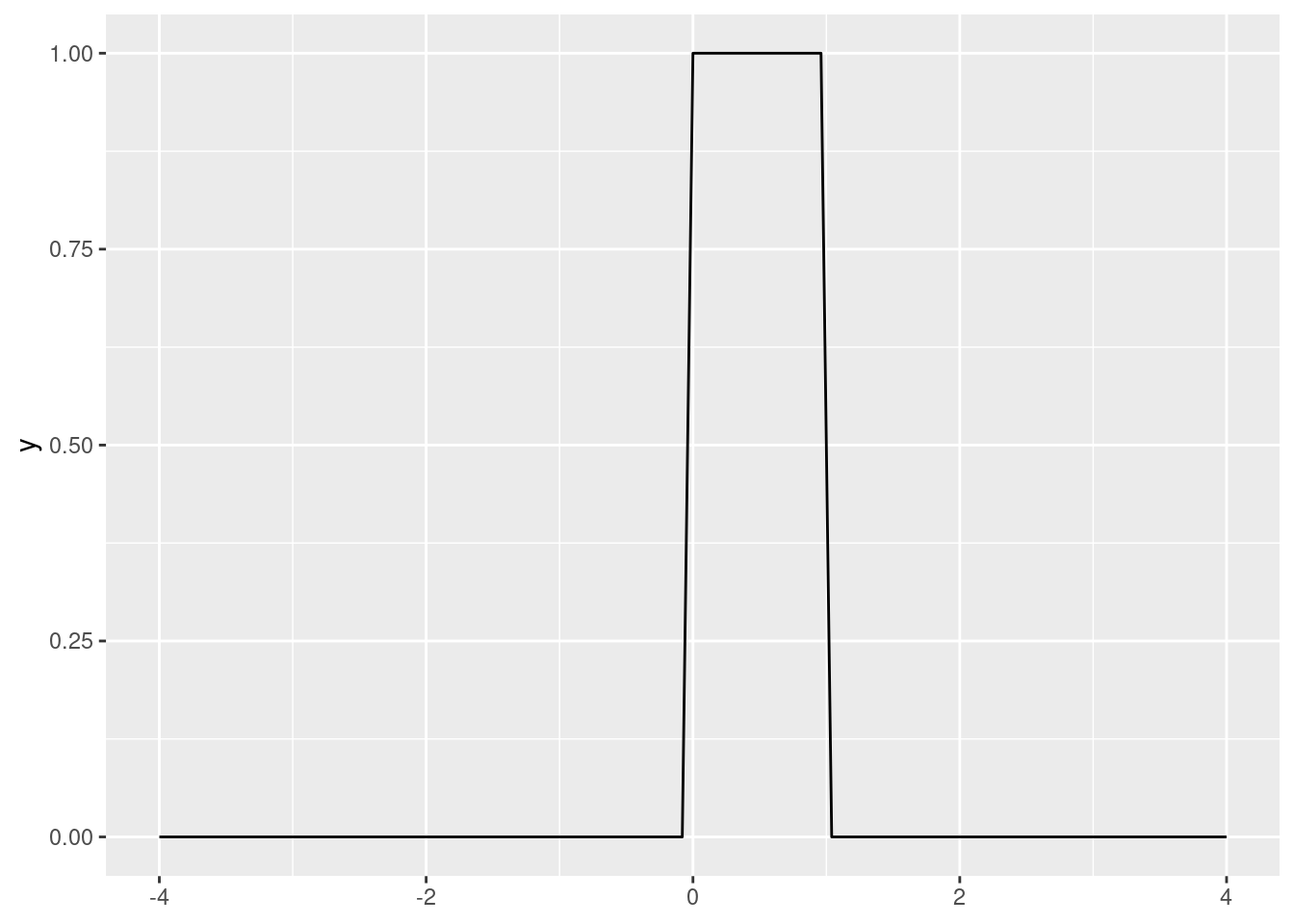

Meanwhile, punif() evaluates the CDF of a uniform distribution.

punif(q = .3)
[1] 0.3
Exercise

Evaluate the CDF of \(Y \sim U(-2, 2)\) at point \(y = 1\). Use the formula and punif().

7.1.4.3 Normal distribution

A normal distribution has two parameters: a mean and a standard deviation. So \(X \sim N(\mu, \sigma)\).

  • PDF: \(2 {\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}}\)

In R, dnorm() gives us the PDF of a standard normal distribution (\(Z \sim N(0, 1)\)):

ggplot() +
  stat_function(fun = dnorm, xlim = c(-4, 4))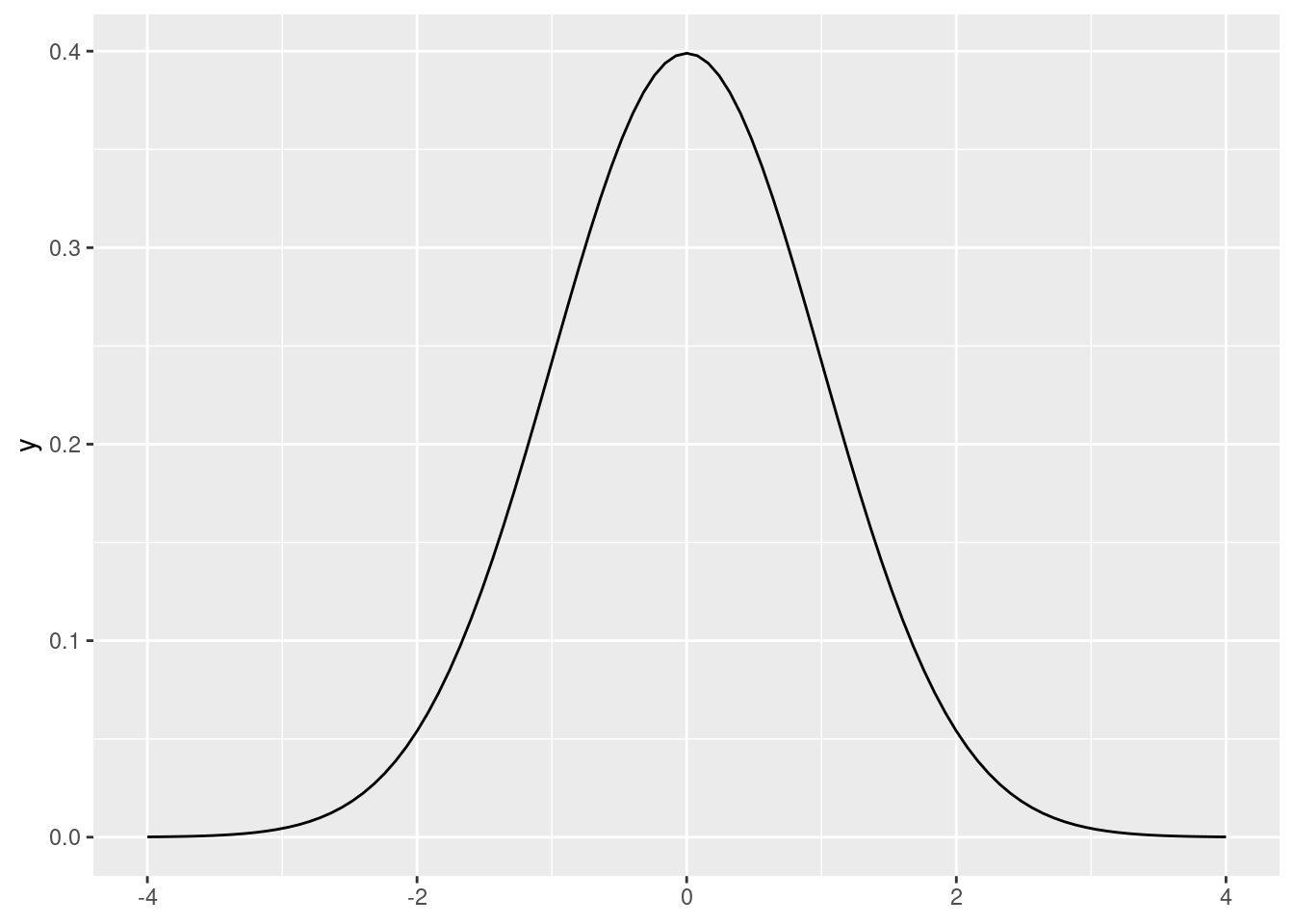

Like you might expect, pnorm() computes the CDF of a normal distribution (by default, the standard normal).

pnorm(0)
[1] 0.5
pnorm(1) - pnorm(-1)
[1] 0.6826895
Exercise

What is the probability of obtaining a value above 1.96 or below -1.96 in a standard normal probability distribution? Hint: use the pnorm() function.

7.2 Statistics

The problems considered by probability and statistics are inverse to each other. In probability theory we consider some underlying process which has some randomness or uncertainty modeled by random variables, and we figure out what happens. In statistics we observe something that has happened, and try to figure out what underlying process would explain those observations. (quote attributed to Persi Diaconis)

  • In statistics we try to learn about a data-generating process (DGP) using our observed data. Example: GDP statistics.

  • Usually we are restrained to samples, while our DGPs of interest are population-based.

    • So we use random sampling or refer to superpopulations as a way to justify how the data we observe can reasonably approximate the population.

  • Statistics has two main targets:

    • Estimation: how we find a reasonable guess of an unknown property (parameter) of a DGP
    • Inference: how we describe uncertainty about our estimate

  • We use an estimator (\(\hat\theta\)), which is a function that summarizes data, as guess about a parameter \(\theta\).

  • Theoretical statistics is all about finding “good” estimators (let’s see an example of different estimators). A few properties of good estimators:

    • Unbiasedness: Across multiple random samples, an unbiased estimator gets the right answer on average.
    • Low variance: Across multiple random samples, a low-variance estimator is more concentrated around the true parameter.
    • BUT it’s usually hard to get both unbiasedness and low variance. We usually quantify this via the mean squared error: \(MSE = bias^2 + variance\). Comparing two estimators, the one with the lowest MSE is said to be more efficient.
    • Consistency: A consistent estimator converges in probability to the true value. “If we had enough data, the probability that our estimate would be far from the truth would be close to zero” (Aronow and Miller 2019, p. 105).

  • Applied statistics is about using these techniques reasonably in messy real-world situations…

7.3 Simulations

  • In simulations, we generate fake data following standard procedures. Why?
    • To better understand how our estimators work in different settings (the methods reason)
    • To get insights about complex processes with many moving parts (the substantive reason) (let’s talk about gerrymandering).

Before we jump into an example, we’ll review some R tools that will build up to simulations.

7.3.1 Random sampling from data

In this module we will work with good ol’ mtcars, one of R’s most notable default datasets. We’ll assign it to an object so it shows in our Environment pane:

my_mtcars <- mtcars
Tip

Default datasets such as mtcars and iris are useful because they are available to everyone, and once you become familiar with them, you can start thinking about the code instead of the intricacies of the data. These qualities also make default datasets ideal for building reproducible examples (see Wickham 2014)

We can use the function sample() to obtain random values from a vector. The size = argument specifies how many values we want. For example, let’s get one random value of the “mpg” column:

sample(my_mtcars$mpg, size = 1)
[1] 21.4

Every time we run this command, we can get a different result:

sample(my_mtcars$mpg, size = 1)
[1] 15.2
sample(my_mtcars$mpg, size = 1)
[1] 15.2

In some occasions we do want to get the same result consistently after running some random process multiple times. In this case, we set a seed, which takes advantage of R’s pseudo-random number generator capabilities. No matter how many times we run the following code block, the result will be the same:

set.seed(123)
sample(my_mtcars$mpg, size = 1)
[1] 15

Sampling with replacement means that we can get the same value multiple times. For example:

set.seed(12)
sample(c("Banana", "Apple", "Orange"), size = 3, replace = T)
[1] "Apple"  "Apple"  "Orange"
sample(my_mtcars$mpg, size = 100, replace = T)
  [1] 26.0 15.2 18.7 18.7 30.4 21.0 24.4 26.0 32.4 15.8 32.4 19.2 18.1 16.4 19.2
 [16] 27.3 14.3 10.4 17.3 13.3 21.4 13.3 19.2 24.4 15.0 27.3 17.8 15.2 15.8 14.3
 [31] 19.7 16.4 18.7 15.8 19.2 21.0 14.3 15.2 14.3 27.3 21.4 33.9 33.9 21.4 30.4
 [46] 33.9 21.4 17.3 17.3 10.4 26.0 18.7 15.2 30.4 10.4 10.4 15.5 14.3 26.0 17.3
 [61] 33.9 26.0 24.4 18.7 30.4 32.4 21.5 30.4 15.2 27.3 13.3 17.3 21.4 24.4 13.3
 [76] 22.8 33.9 13.3 21.5 14.3 19.2 30.4 24.4 26.0 15.8 10.4 24.4 14.3 15.2 10.4
 [91] 19.2 21.0 16.4 19.2 24.4 19.7 18.7 10.4 18.7 17.8

In order to sample not from a vector but from a data frame’s rows, we can use the slice_sample() function from dplyr:

my_mtcars |> 
  slice_sample(n = 2) # a number of rows
                  mpg cyl disp  hp drat   wt  qsec vs am gear carb
Dodge Challenger 15.5   8  318 150 2.76 3.52 16.87  0  0    3    2
Datsun 710       22.8   4  108  93 3.85 2.32 18.61  1  1    4    1
my_mtcars |> 
  slice_sample(prop = 0.5) # a proportion of rows
                     mpg cyl  disp  hp drat    wt  qsec vs am gear carb
Toyota Corolla      33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1
Ferrari Dino        19.7   6 145.0 175 3.62 2.770 15.50  0  1    5    6
Merc 450SE          16.4   8 275.8 180 3.07 4.070 17.40  0  0    3    3
Hornet Sportabout   18.7   8 360.0 175 3.15 3.440 17.02  0  0    3    2
Maserati Bora       15.0   8 301.0 335 3.54 3.570 14.60  0  1    5    8
Datsun 710          22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
Ford Pantera L      15.8   8 351.0 264 4.22 3.170 14.50  0  1    5    4
Dodge Challenger    15.5   8 318.0 150 2.76 3.520 16.87  0  0    3    2
Merc 280            19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
Lincoln Continental 10.4   8 460.0 215 3.00 5.424 17.82  0  0    3    4
Valiant             18.1   6 225.0 105 2.76 3.460 20.22  1  0    3    1
Fiat 128            32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
Mazda RX4 Wag       21.0   6 160.0 110 3.90 2.875 17.02  0  1    4    4
Merc 240D           24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
Camaro Z28          13.3   8 350.0 245 3.73 3.840 15.41  0  0    3    4
Cadillac Fleetwood  10.4   8 472.0 205 2.93 5.250 17.98  0  0    3    4

Again, we can also use seeds here to ensure that we’ll get the same result each time:

set.seed(123)
my_mtcars |> 
  slice_sample(prop = 0.5)
                    mpg cyl  disp  hp drat    wt  qsec vs am gear carb
Maserati Bora      15.0   8 301.0 335 3.54 3.570 14.60  0  1    5    8
Cadillac Fleetwood 10.4   8 472.0 205 2.93 5.250 17.98  0  0    3    4
Honda Civic        30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
Merc 450SLC        15.2   8 275.8 180 3.07 3.780 18.00  0  0    3    3
Datsun 710         22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
Merc 280           19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
Fiat 128           32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
Dodge Challenger   15.5   8 318.0 150 2.76 3.520 16.87  0  0    3    2
Merc 280C          17.8   6 167.6 123 3.92 3.440 18.90  1  0    4    4
Hornet Sportabout  18.7   8 360.0 175 3.15 3.440 17.02  0  0    3    2
Toyota Corolla     33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1
Ford Pantera L     15.8   8 351.0 264 4.22 3.170 14.50  0  1    5    4
AMC Javelin        15.2   8 304.0 150 3.15 3.435 17.30  0  0    3    2
Ferrari Dino       19.7   6 145.0 175 3.62 2.770 15.50  0  1    5    6
Merc 230           22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
Lotus Europa       30.4   4  95.1 113 3.77 1.513 16.90  1  1    5    2

And we can also sample with replacement:

set.seed(123)
my_mtcars |> 
  slice_sample(prop = 1, replace = T)
                        mpg cyl  disp  hp drat    wt  qsec vs am gear carb
Maserati Bora          15.0   8 301.0 335 3.54 3.570 14.60  0  1    5    8
Cadillac Fleetwood     10.4   8 472.0 205 2.93 5.250 17.98  0  0    3    4
Honda Civic...3        30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
Merc 450SLC...4        15.2   8 275.8 180 3.07 3.780 18.00  0  0    3    3
Datsun 710...5         22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
Merc 280...6           19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
Fiat 128               32.4   4  78.7  66 4.08 2.200 19.47  1  1    4    1
Dodge Challenger...8   15.5   8 318.0 150 2.76 3.520 16.87  0  0    3    2
Merc 280C              17.8   6 167.6 123 3.92 3.440 18.90  1  0    4    4
Hornet Sportabout...10 18.7   8 360.0 175 3.15 3.440 17.02  0  0    3    2
Toyota Corolla         33.9   4  71.1  65 4.22 1.835 19.90  1  1    4    1
Merc 450SLC...12       15.2   8 275.8 180 3.07 3.780 18.00  0  0    3    3
Dodge Challenger...13  15.5   8 318.0 150 2.76 3.520 16.87  0  0    3    2
Pontiac Firebird...14  19.2   8 400.0 175 3.08 3.845 17.05  0  0    3    2
Fiat X1-9...15         27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
Porsche 914-2...16     26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2
Volvo 142E             21.4   4 121.0 109 4.11 2.780 18.60  1  1    4    2
Hornet Sportabout...18 18.7   8 360.0 175 3.15 3.440 17.02  0  0    3    2
Honda Civic...19       30.4   4  75.7  52 4.93 1.615 18.52  1  1    4    2
Porsche 914-2...20     26.0   4 120.3  91 4.43 2.140 16.70  0  1    5    2
Pontiac Firebird...21  19.2   8 400.0 175 3.08 3.845 17.05  0  0    3    2
Lotus Europa           30.4   4  95.1 113 3.77 1.513 16.90  1  1    5    2
Pontiac Firebird...23  19.2   8 400.0 175 3.08 3.845 17.05  0  0    3    2
Merc 230...24          22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
Ford Pantera L         15.8   8 351.0 264 4.22 3.170 14.50  0  1    5    4
Datsun 710...26        22.8   4 108.0  93 3.85 2.320 18.61  1  1    4    1
Merc 240D              24.4   4 146.7  62 3.69 3.190 20.00  1  0    4    2
Fiat X1-9...28         27.3   4  79.0  66 4.08 1.935 18.90  1  1    4    1
Duster 360             14.3   8 360.0 245 3.21 3.570 15.84  0  0    3    4
Merc 280...30          19.2   6 167.6 123 3.92 3.440 18.30  1  0    4    4
Merc 230...31          22.8   4 140.8  95 3.92 3.150 22.90  1  0    4    2
Ferrari Dino           19.7   6 145.0 175 3.62 2.770 15.50  0  1    5    6

7.3.2 Random sampling from theoretical distributions

We can also draw sample numbers from theoretical distributions.

Uniform distribution

For the uniform distribution, the arguments specify how many draws we want and the boundaries

runif(n = 20, min = -3, max = 3)
 [1]  1.1442317  1.7728045 -2.8523179 -0.1332242  1.5507572 -1.7015524
 [7] -1.0909140 -1.6102453 -2.1431999 -0.5127220 -0.5176540 -0.7869273
[13] -2.0853315 -2.1671636 -1.6017954 -0.2042253 -1.4041642  2.1469663
[19] -2.7250130 -0.3467996

When we draw a million times from the distribution, we can then plot it and see that it does look as we would expect:

set.seed(123)
my_runif <- runif(n = 1000000, min = -3, max = 3)
ggplot(data.frame(my_runif), aes(x = my_runif)) +
  geom_histogram(binwidth = 0.25, boundary = 0, closed = "right") +
  scale_x_continuous(breaks = seq(-5, 5, 1), limits = c(-5, 5))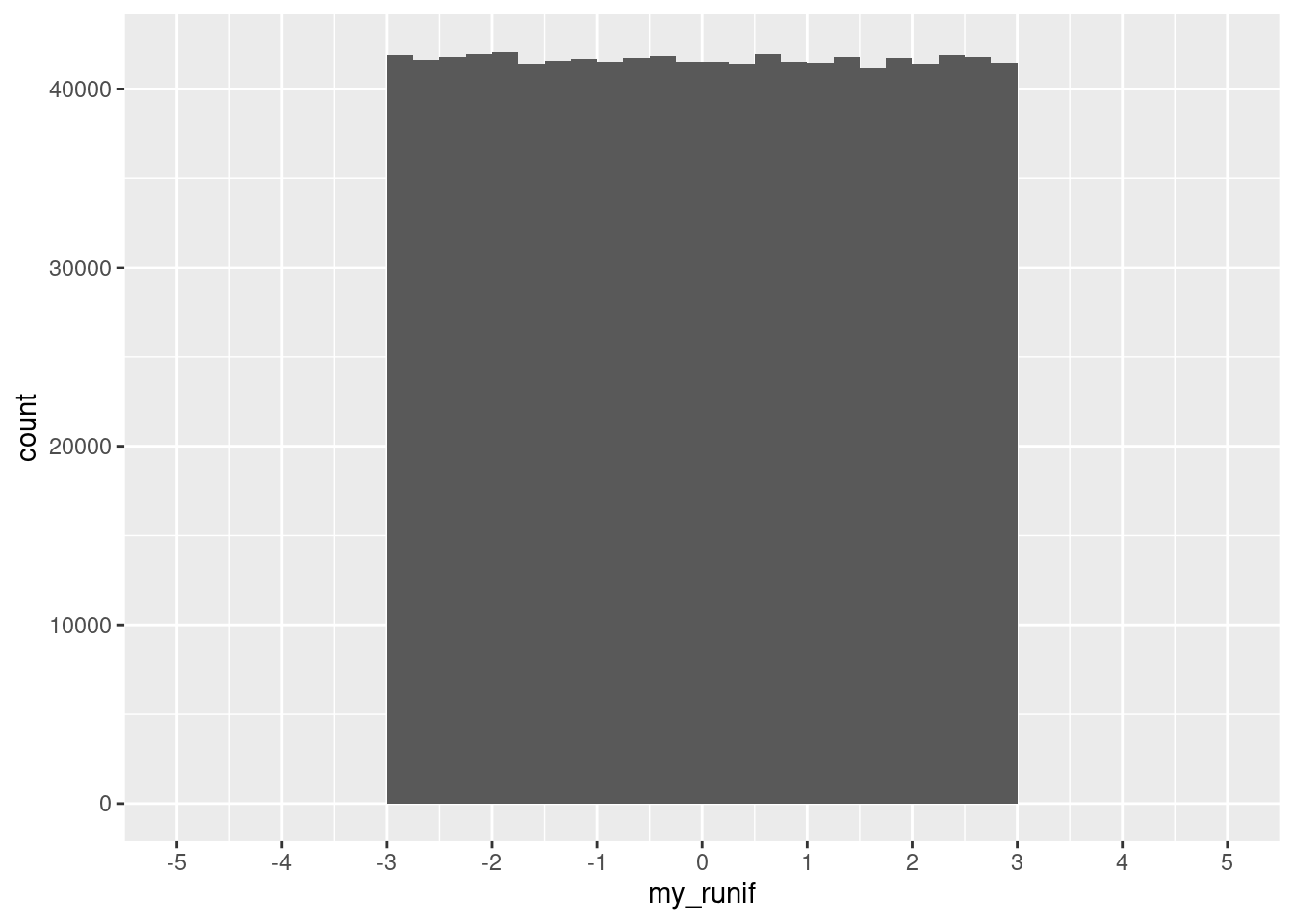

Binomial distribution

For the binomial distribution, we can specify the number of draws, how many trials each draw will have, and the probability of success.

For instance, we can ask R to do the following twenty times: flip a fair coin one hundred times, and count the number of tails.

rbinom(n = 20, size = 100, prob = 0.5)
 [1] 48 45 54 50 58 50 42 58 48 57 53 49 52 51 49 40 57 53 52 41

With prob = , we can implement unfair coins:

rbinom(n = 20, size = 100, prob = 0.9)
 [1] 88 87 93 95 93 92 91 94 87 91 90 92 93 89 90 95 91 90 86 88

Normal distribution

For the Normal or Gaussian distribution, we specify the number of draws, the mean, and standard deviation:

rnorm(n = 20, mean = 0, sd = 1)
 [1]  1.10455864  0.06386693 -1.59684275  1.86298270 -0.90428935 -1.55158044
 [7]  1.27986282 -0.32420495 -0.70015076  2.17271578  0.89778913 -0.01338538
[13] -0.74074395  0.36772316 -0.66453402 -1.11498344 -1.15067439 -0.55098894
[19]  0.10503154 -0.27183645
Exercise

Compute and plot my_rnorm, a vector with one million draws from a Normal distribution \(Z\) with mean equal to zero and standard deviation equal to one (\(Z\sim N(0,1)\)). You can recycle code from what we did for the uniform distribution!

7.3.3 Loops

Loops allow us to repeat operations in R. The most common construct is the for-loop:

for (i in 1:10){
  print(i)
}
[1] 1
[1] 2
[1] 3
[1] 4
[1] 5
[1] 6
[1] 7
[1] 8
[1] 9
[1] 10

We talked about loops and various extensions in one of our methods workshops last year: Speedy R.

7.3.4 An example simulation: bootstrapping a sample mean

Bootstrap (and its relatives) is one way in which we can do inference. We’ll go through the intuition on the board.

bootstrapped_means <- vector(mode = "numeric", length = 10000)
for (i in 1:10000){
  m <- my_mtcars |> slice_sample(prop = 1, replace = T)
  bootstrapped_means[i] <- mean(m$mpg)
}
ggplot(data.frame(bootstrapped_means), aes(x = bootstrapped_means)) +
  geom_histogram(binwidth = 0.25, boundary = 0, closed = "right")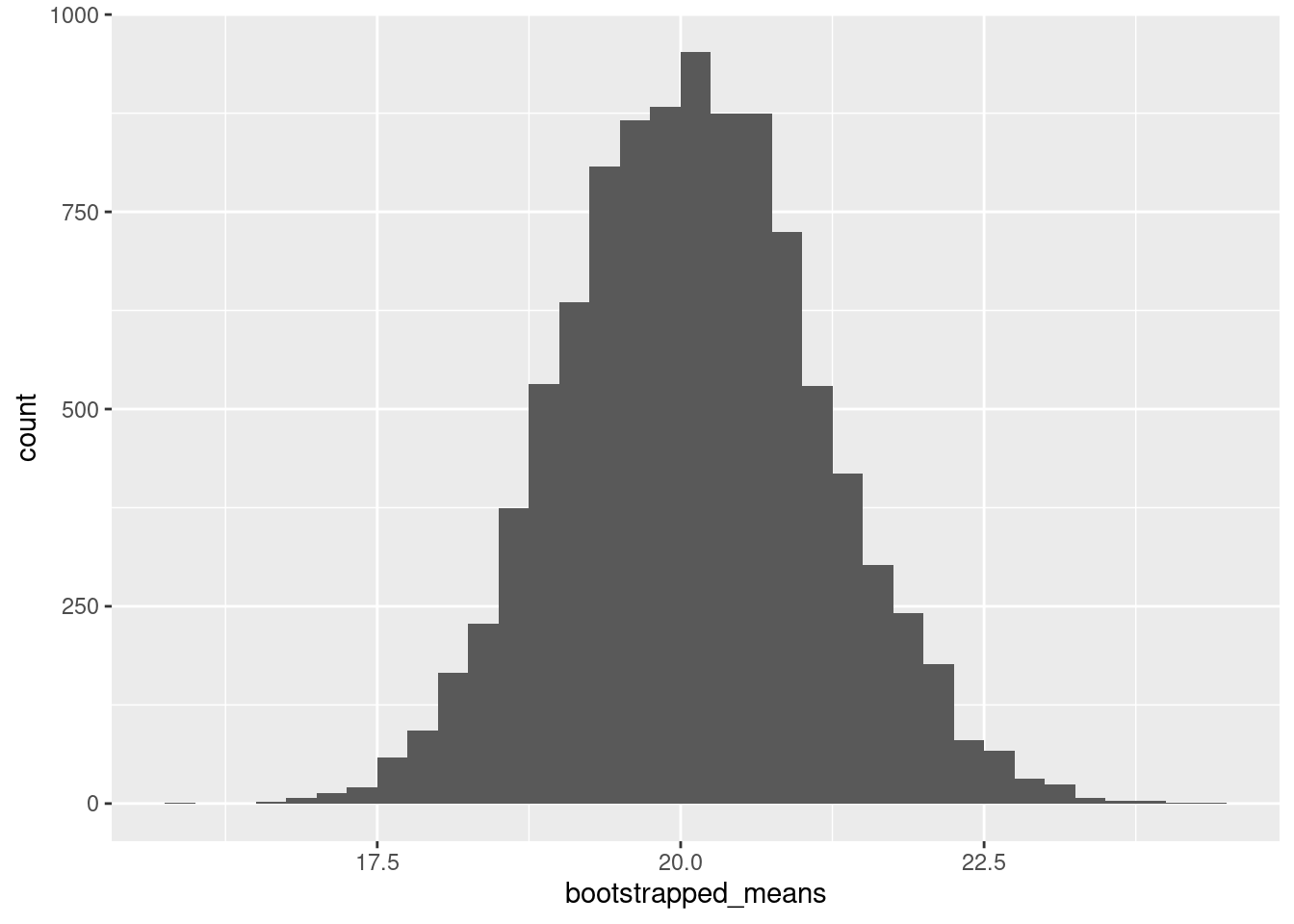

  1. This is sometimes called the frequentist interpretation of probability. There are other possibilities, such as Bayesian interpretations of probability, which describe probabilities as degrees of belief.↩︎