dbinom(x = 0, size = 100, prob = 0.02)[1] 0.13261967 Probability
7.1 What is probability?
- Informally, a probability is a number that describes how likely an event is.
- It is, by definition, between 0 and 1.
- What is the probability that a fair coin flip will result in heads?
- We can also think of a probability as an outcome’s relative frequency after repeating an “experiment” many times.1
- In this setting, an experiment is “an action or a set of actions that produce stochastic [random] events of interest” (Imai and Williams 2022, p. 281). Not to confuse with scientific experiments!
- If we were to flip a million fair coins, what will be the proportion of heads?
- A probability space \((\Omega, S, P)\) is a formal way to talk about a random process:
- The sample space (\(\Omega\)) is the set of all possible outcomes.
- The event space (\(S\)) is a collection of events (an event is a subset of \(\Omega\)).
- The probability measure (\(P\)) is a function that assigns a probability in \(\mathbb{R}\) to every event in \(S\). So \(P: S \rightarrow \mathbb{R}\).
- We can formalize our intuitions with the probability axioms (sometimes called Kolmogorov’s axioms):
- \(P(A) \ge 0, \; \forall A \in S\).
- Probabilities must be non-negative.
- \(P(\Omega) = 1\).
- Something has to happen!
- Probabilities sum/integrate to 1.
- \(P(A \cup B) = P(A) + P(B), \; \forall A, B \in S, \; A\cup B = \emptyset\).
- The probability of disjoint (mutually exclusive) events is equal to the sum of their individual probabilities.
- \(P(A) \ge 0, \; \forall A \in S\).
7.2 Definitions and properties of probability
Joint probability: \(P(A \cap B)\). The probability that the two events will occur in one realization of the experiment.
Law of total probability: \(P(A) = P(A \cap B) + P(A \cap B^C)\).
Addition rule: \(P(A \cup B) = P(A) + P(B) - P (A \cap B)\).
Conditional probability: \(\displaystyle P(A|B)=\frac{P(A \cap B)}{P(B)}\)
- the probability of event \(A\) occurring given that event \(B\) has already occurred is the probability that both \(A\) and \(B\) occur together devided by the probability that event \(B\) occurs
Bayes theorem: \(\displaystyle P(A|B) = \frac{P(A) \cdot P(B|A)}{P(B)}\)
- \(P(A|B)\): the probability of event A occurring given that B is true
- \(P(B|A)\): the probability of event B occurring given that A is true.
7.3 Random variables and probability distributions
A random variable is a function (\(X: \Omega \to \mathbb{R}\)) of the outcome of a random generative process. Informally, it is a “placeholder” for whatever will be the output of a process we’re studying.
A probability distribution describes the probabilities associated with the values of a random variable.
Random variables (and probability distributions) can be discrete or continuous.
7.3.1 Discrete random variables and probability distributions
A sample space in which there are a (finite or infinite) countable number of outcomes
Each realization of random process has a discrete probability of occurring.
- \(f(X=x_i)=P(X=x_i)\) is the probability the variable takes the value \(x_i\).
An example
What’s the probability that we’ll roll a 3 on one die roll: \[Pr(y=3) = \dfrac{1}{6}\]
If one roll of the die is an “experiment,” we can think of a 3 as a “success.”
\(Y \sim Bernoulli \left(\frac{1}{6} \right)\)
Fair coins are \(\sim Bernoulli(.5)\), for example.
More generally, \(Bernoulli(\pi )\). We’ll talk about other probability distributions soon.
- \(\pi\) represents the probability of success.
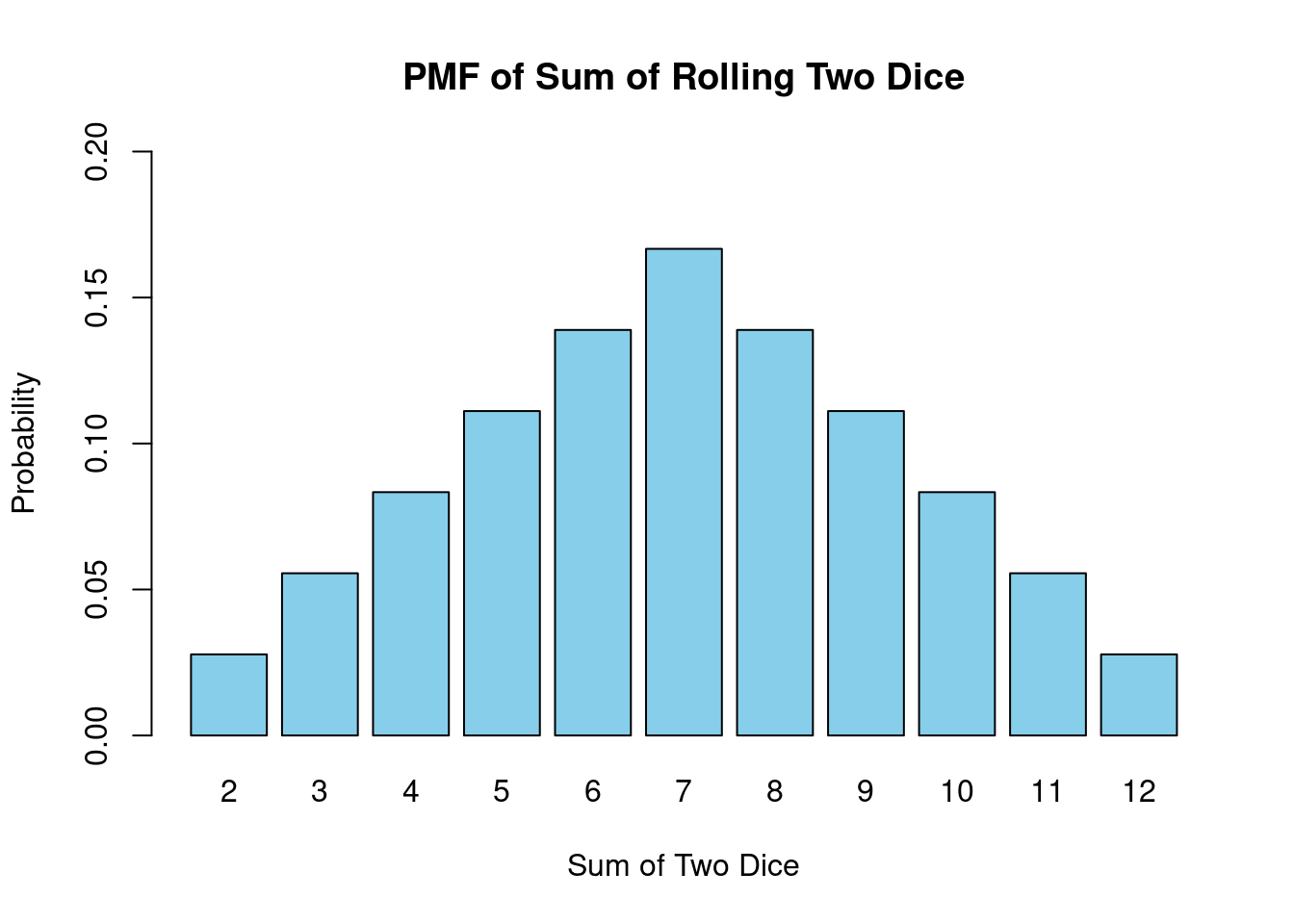
Let’s do another example on the board, using the sum of two fair dice.
Exercise:
What’s the probability that the sum of two fair dice equals 7?
7.3.2 Continuous random variables and probability distributions
- What happens when our outcome is continuous?
- There are an infinite number of outcomes. This makes the denominator of our fraction difficult to work with.
- The probability of the whole space must equal 1.
- The domain may not span -\(\infty\) to \(\infty\).
- Even space between 0 and 1 is infinite!
- Two common examples are the uniform and normal probability distributions, which we will discuss below.
7.4 Functions describing probability distributions
7.4.1 Probability Mass Function (PMF) – Discrete Variables
Probability of each occurrence encoded in probability mass function (PMF)
\(0 \leq f(x_i) \leq 1\): Probability of any value occurring must be between 0 and 1.
\(\displaystyle\sum_{x}f(x_i) = 1\): Probabilities of all values must sum to 1.
7.4.2 Probability Density Function (PDF) – Continuous Variables
Similar to PMF from before, but for continuous variables.
Using integration, it gives the probability a value falls within a particular interval
\[P[a\le X\le b] = \displaystyle\int_a^b f(x) \, dx\]
Total area under the curve is 1.
\(P(a < X < b)\) is the area under the curve between \(a\) and \(b\) (where \(b > a\)).
Source: Wikipedia Commons
7.4.3 Cumulative Density Function (CDF)
Discrete
- Cumulatve density function is probability X will take a value of x or lower.
- PDF is written \(f(x)\), and CDF is written \(F'(x)\). \[F_X(x) = Pr(X\leq x)\]
- For discrete CDFs, that means summing up over all values.
Exercise:
What is the probability of rolling a 6 or lower with two dice? \(F(6)=?\)
Continuous
- We can’t sum probabilities for continuous distributions (remember the 0 problem).
- Solution: integration \[F_Y(y) = \int_{-\infty}^{y} f(y) dy\]
- Examples of uniform distribution.
7.5 Common types of probability distributions
There are many useful probability distributions. In this section we will cover three of the most common ones: the binomial, uniform, and normal distributions.
7.5.1 Binomial distribution
A Binomial distribution is defined as follow: \(X \sim Binomial(n, p)\)
PMF:
\[ {n \choose k} p^k(1-p)^{n-k} \] , where \(n\) is the number of trials, \(p\) is the probability of success, and \(k\) is the number of successes.
Remember that:
\[ {n \choose k} = \frac{n!}{k!(n-k)!} \]
For example, let’s say that voters choose some candidate with probability 0.02. What is the probability of seeing exactly 0 voters of the candidate in a sample of 100 people?
We can compute the PMF of a binomial distribution using R’s dbinom() function.
dbinom(x = 1, size = 100, prob = 0.02)[1] 0.2706522Similarly, we can compute the CDF using R’s pbinom() function:
pbinom(q = 0, size = 100, prob = 0.02)[1] 0.1326196pbinom(q = 100, size = 100, prob = 0.02)[1] 1pbinom(q = 1, size = 100, prob = 0.02)[1] 0.4032717
Exercise
Compute the probability of seeing between 1 and 10 voters of the candidate in a sample of 100 people.
7.5.2 Uniform distribution
A uniform distribution has two parameters: a minimum and a maximum. So \(X \sim U(a, b)\).
- PDF:
\[ \displaystyle{ \begin{cases} \frac{1}{b-a} & \text{, }{x \in [a, b]}\\ 0 & \text{, otherwise} \end{cases} } \]
- CDF:
\[ \displaystyle{ \begin{cases} 0 & \text{, }{x < a}\\ \frac{x-a}{b-a} & \text{, }{x \in [a, b]}\\ 1 & \text{, }{x>b} \end{cases} } \]
In R, dunif() gives the PDF of a uniform distribution. By default, it is \(X \sim U(0, 1)\).
library(tidyverse)ggplot() +
stat_function(fun = dunif, xlim = c(-4, 4))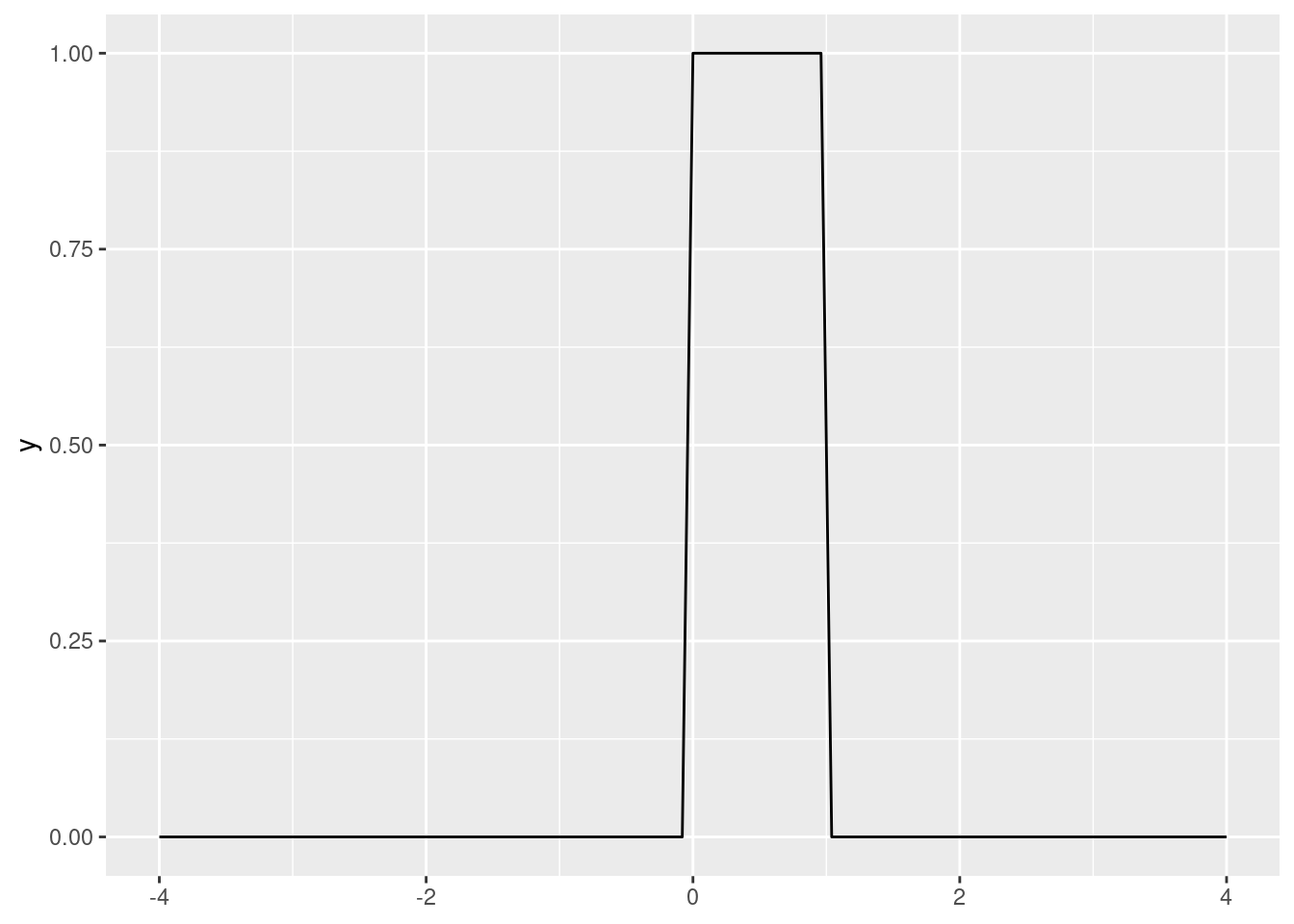
Meanwhile, punif() evaluates the CDF of a uniform distribution.
punif(q = .3)[1] 0.3
Exercise
Evaluate the CDF of \(Y \sim U(-2, 2)\) at point \(y = 1\). Use the formula and punif().
7.5.3 Normal distribution
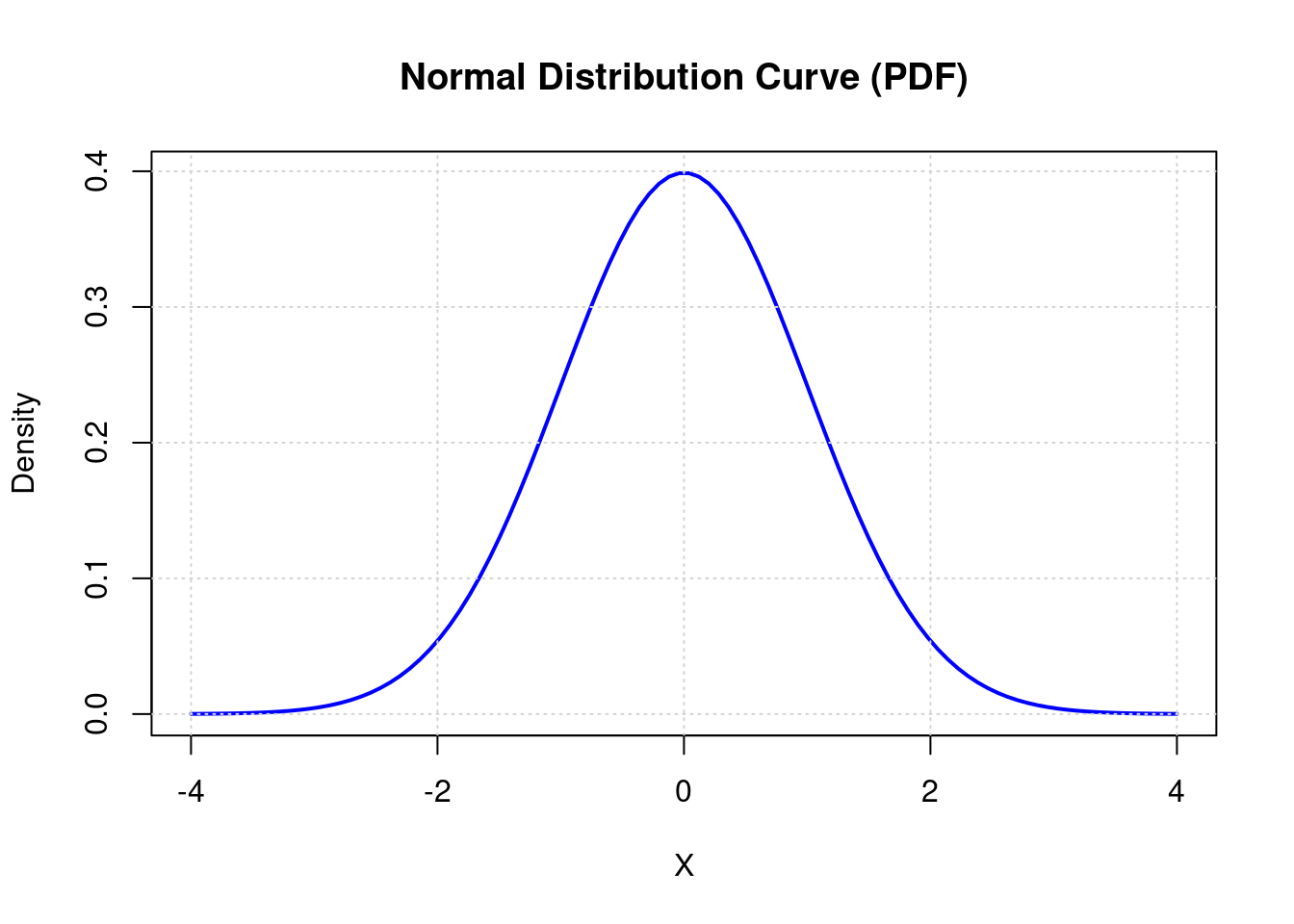
A normal distribution has two parameters: a mean and a standard deviation. So \(X \sim N(\mu, \sigma)\).
- PDF: \(2 {\displaystyle {\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}}\)
In R, dnorm() gives us the PDF of a standard normal distribution (\(Z \sim N(0, 1)\)):
ggplot() +
stat_function(fun = dnorm, xlim = c(-4, 4))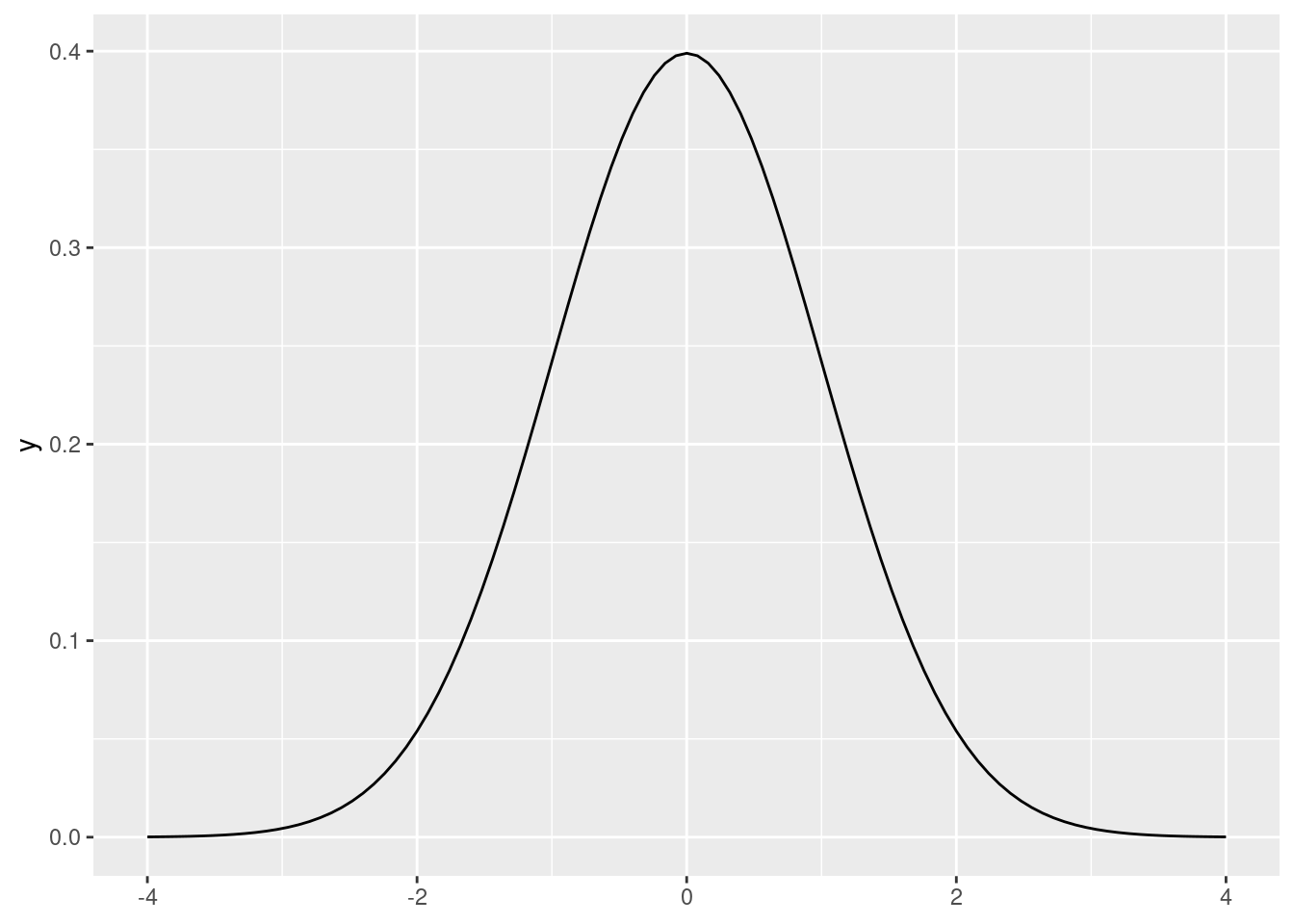
Like you might expect, pnorm() computes the CDF of a normal distribution (by default, the standard normal).
pnorm(0)[1] 0.5pnorm(1) - pnorm(-1)[1] 0.6826895
Exercise
What is the probability of obtaining a value above 1.96 or below -1.96 in a standard normal probability distribution? Hint: use the pnorm() function.
This is sometimes called the frequentist interpretation of probability. There are other possibilities, such as Bayesian interpretations of probability, which describe probabilities as degrees of belief.↩︎